Demystifying Artificial Intelligence - Understanding the Basics Part III

However, the surprisingly powerful functioning of AI systems raises a crucial question:
Why does AI work so well?
In this blog post, we will explore the underlying reasons behind the success of AI algorithms and provide a simple explanation of their effectiveness.
At the core of neural networks is their remarkable ability to approximate any function. This ability is supported by the Universal Approximation Theorem, which states that a neural network with just a single hidden layer can approximate any continuous function. In simple terms, it means that a neural network can learn and represent any complex relationship between inputs and outputs with high accuracy.
To illustrate this concept, let’s consider an example of approximating a sales graph as shown below using a neural network.
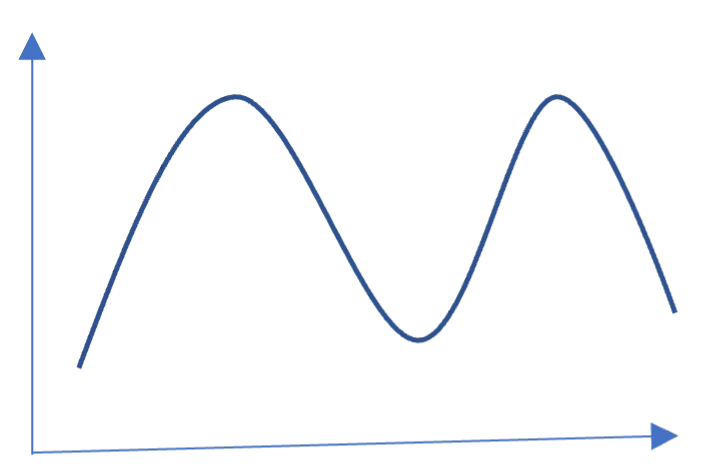
The neural network takes would predict the sales value as depicted on the y-axis.
According to the universality theorem, the neural network can approximate any continuous function reasonably well. This implies that, given any continuous function $f(x)$, where x belongs to the set of real numbers
$$ f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$$
A neural network can find an approximation
$$ g: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$$
such that the difference between $f(x)$ and $g(x)$ is less than a specified tolerance. The norm is used to refer to any distance metric such as Euclidean distance.
$$|g(x) - f(x)|$$
While the formal definition of the universality theorem may seem abstract, we will visualize its concept using a simple neural network with pairs of nodes, a single hidden layer, and one input. By leveraging this minimal architecture, the neural network can approximate univariate functions with remarkable accuracy. This showcases the incredible flexibility and power of neural networks in modeling complex relationships between variables.
Let’s consider a simple scenario where we have a single input node passing its weight to a hidden layer with a pair of nodes. At the hidden nodes, a bias term is added, followed by the application of an activation function, such as the sigmoid function, which maps the output to a range between 0 and 1.

By manipulating the weight and bias values, we can observe changes in the shape of the output curve. Decreasing the weight widens the sigmoid curve, while increasing the weight makes it steeper. On the other hand, adjusting the bias term does not alter the curve’s shape but shifts the point at which the step (or breakpoint) occurs.
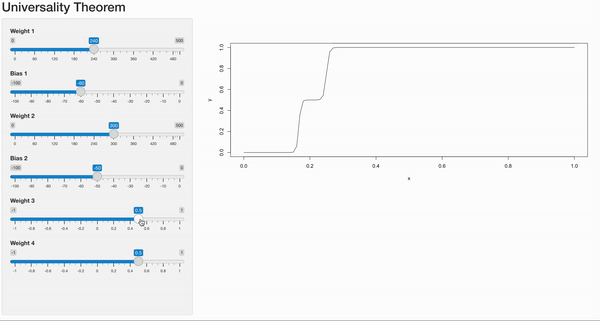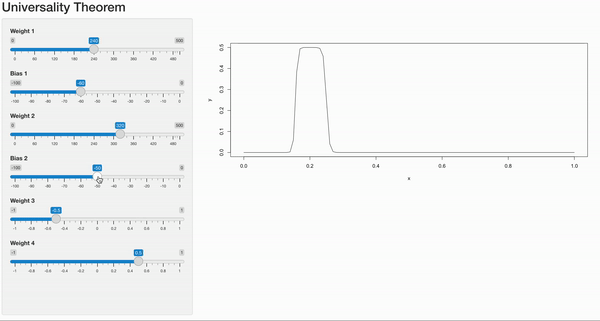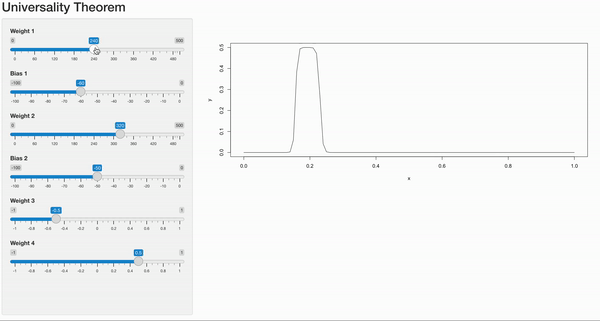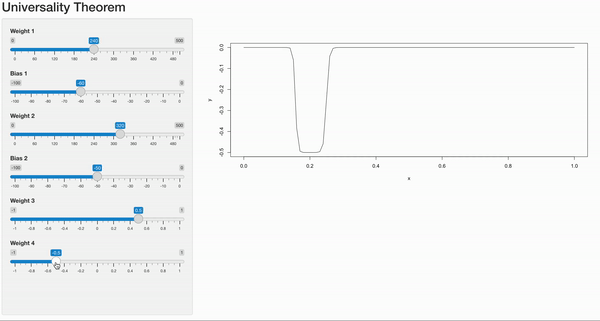
With just a pair of hidden neuron, we can create a step function as shown in the gif. But when we combine multiple pairs of hidden neurons, each with its own weight and bias values, we can generate a curve based on histogram-like structures. By tweaking the weights and biases, we control the height and width of each bar in the histogram.

By increasing the number of hidden neurons in a single hidden neural network, we can generate multiple bars together, effectively approximating any continuous function. This process resembles the operation of a Riemann Integral, where the area under the curve is computed by dividing it into small bars. The back propagation process tweaks the weights and biases such that the neural networks approximates the underlying function well. The proof can be extended to higher dimensions as well.
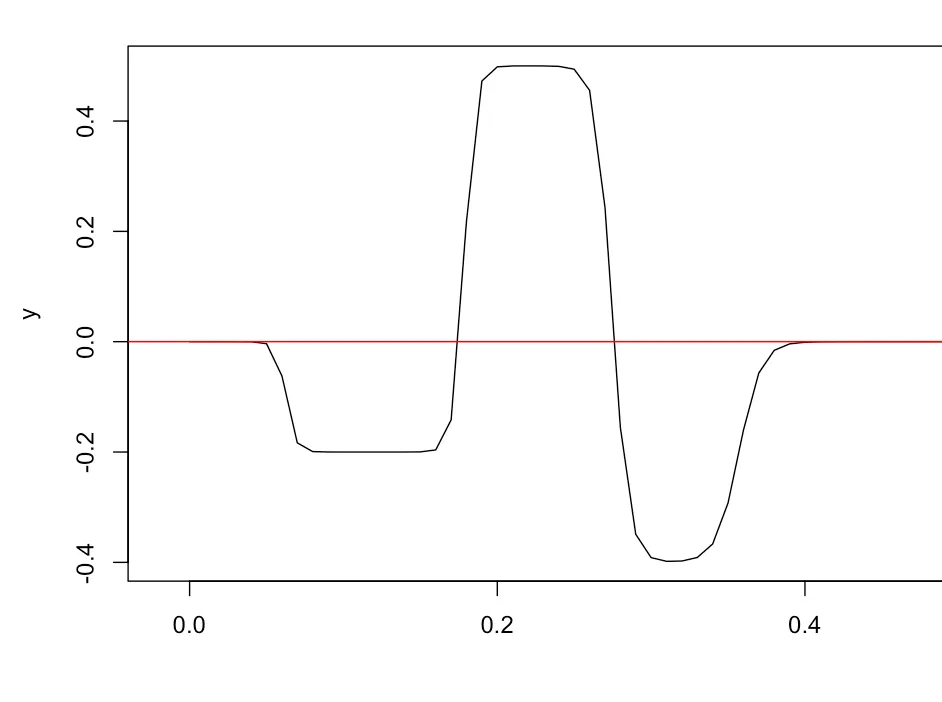
It’s fascinating to see how the collective behavior of these hidden neurons enables a neural network to approximate complex functions and capture intricate relationships within the data. This fundamental property of neural networks, coupled with their ability to learn and adapt through the back propagation process, is what makes them so powerful in the field of AI.
As we continue to explore and refine the architecture and training methods of neural networks, we unlock even greater potential for AI algorithms to solve increasingly complex problems and advance various domains, ranging from healthcare and finance to transportation and entertainment.
In the world of AI, the interplay between the weights, biases, and activation functions within neural networks is like an intricate dance, enabling machines to mimic human-like intelligence and achieve remarkable feats. So, the next time you encounter an AI system making accurate predictions or solving complex tasks, remember the underlying beauty of these hidden neurons working together to approximate the continuous functions that power our AI-driven world.
Conclusion:
In conclusion, the effectiveness of AI algorithms can be attributed to the power of Artificial Neural Networks (ANNs) and the Universal Approximation Theorem. ANNs serve as the backbone of AI systems, utilizing their ability to approximate any function with great accuracy. This capability allows neural networks to learn intricate patterns and relationships in data, enabling them to perform tasks that were once thought to be within the realm of human intelligence.



